株式投資をする上で、切り離せないのが「リスク」です。「リスク」とは、マイナス面だけではなく、アップサイドとダウンサイド、双方の変動幅の大小のことを言います。
では、株式投資の「リスク」を減らしたい、と考えたら、みなさんは何をすべきだと考えますか?


このようにリスク軽減=分散投資と考えて間違いはないのですが、なんとなく、単に「たくさんの銘柄を買えばリスク分散になる」と思ってないでしょうか。あるいは、「2つの銘柄を持つだけでは全然リスク分散になってない」と考えてませんか。さらには「株式投資を適切に分散できれば、ほとんどのリスクをコントロールできる」と考えている人もいるかもしれません。


ということで今回は、リスク分散を正しく理解することを目標に解説していきたいと思います。

リスク分散にはまずリスクの種類を知ることが大事
リスクは2種類 マーケットリスクと銘柄固有リスク
株式のトータルリスクは、2つのリスクで構成されています。
1つがマーケットリスクで、システマチックリスクとも言われます。
もう1つが銘柄固有リスクで、アンシステマチックリスクとも言われます。
結論から言うと、マーケットリスクは分散不能なリスク、銘柄固有リスクは分散可能なリスクです。
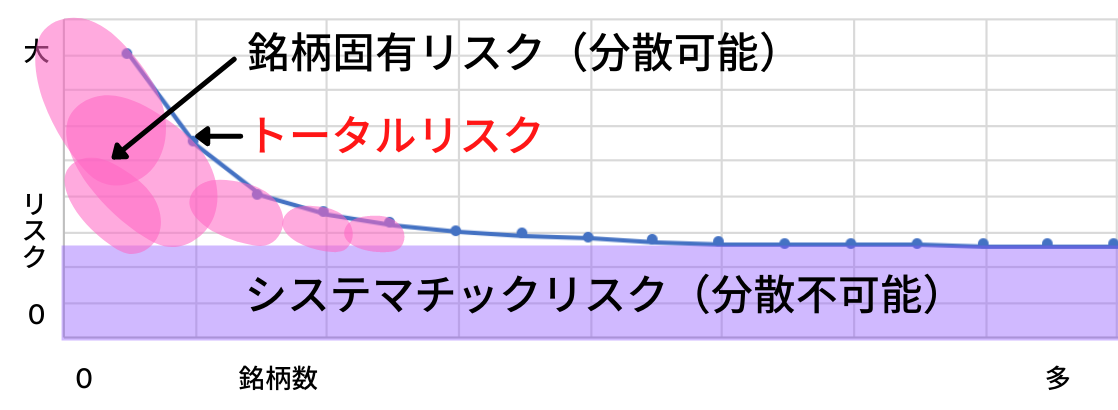
ポートフォリオの分散効果
上図が株式ポートフォリのリスク分散効果の(下手くそな)例です。回避不能なリスクが横たわっていて、その上に銘柄固有リスクが乗っかって、トータルリスクを押し上げていると言う構図です。したがって、トータルリスクを最小化するには銘柄固有リスクを最小化すれば良いと言うことになります。
かのウォーレン・バフェットも「投資家の98%は、分散化された資産ポートフォリオに投資することにより恩恵を得ている」と語っています。
銘柄固有リスクを求める
次は、その分散化された資産ポートフォリオについて正しく理解していきましょう。
ここからは
- 2つの個別銘柄のリスクとリターンを求め、
- それらを掛け合わせたポートフォリオのリスクとリターンを求め、
- 実際にどの程度リスク分散されているかをみていきたいと思います。
個別銘柄のリスクを求める
まず、個別資産のリスクを求めていきます。
景気に連動して業績の良くなるA社と景気とは逆相関のB社を例にします。
| 景気 | 確率 | A社リターン | B社リターン |
| 好況 | 0.3 | 20% | -2% |
| 通常 | 0.55 | 10% | 10% |
| 不況 | 0.15 | -2% | 25% |
景気動向によってリターンが変わるので、景気動向の確率(好況30%、通常55%、不況15%)とそれによって変わるA社、B社それぞれのリターンを上図のようにします。ちょっと極端ですが、あくまでも例なので。
リスク=ばらつき=標準偏差
まずA社のリスクから求めます。
| 景気 | 確率 | リターン | 確率*リターン | 偏差 | 偏差の二乗 |
| 好況 | 0.3 | 20% | 6.0% | 8.80% | 77.44 |
| 通常 | 0.55 | 10% | 5.5% | 10.00% | 100 |
| 不況 | 0.15 | -2% | -0.3% | -2.00% | 4 |
| 期待リターン | 11.2% | リスク | 181.44 | ||
確率×リターンを足し合わせたものが期待リターンとなります。
計算式は6.0%+5.5%+(-0.3%)=11.2%
そして、各景気の時のリターンから期待リターンを引いたものが偏差となります。
好況を例にすると 20%-11.2%=8.80%
偏差を足し合わせてもプラスとマイナスで相殺し合うのでそれができないように偏差を二乗します。好況を例にすると、8.80×8.80=77.44
さらに偏差の二乗の数字をすべて足し合わせます。
77.44+100+4=181.44 これが分散です。
最後に、冪乗の数値を正の平方根に戻す(=ルートを外す=SQRT関数)処理をすると、標準偏差は13.47と出ました(13.47×13.47=181.44 ということです)。これがばらつき、つまりリスクの大きさを示します。
同様にB社を求めます。
| 景気 | 確率 | リターン | 確率*リターン | 偏差 | 偏差の二乗 |
| 好況 | 0.3 | -2% | -0.6% | -10.65% | 113.4225 |
| 通常 | 0.55 | 10% | 5.5% | 10.00% | 100 |
| 不況 | 0.15 | 25% | 3.8% | 25.00% | 625 |
| 期待リターン | 8.7% | 分散 | 838.42 | ||
分散は838.42になりました。最後に冪乗の数値を正の平方根に戻すと、標準偏差は28.96となりました。
B社の方がばらつきが大きいですね。
次に、期待リターン1%あたりのリスクを求めます。
計算式は標準偏差÷期待リターンでこれを変動係数(CV)と呼びます。
| 期待リターン | 標準偏差 | CV | |
| A社 | 11.2% | 13.47 | 1.20 |
| B社 | 8.7% | 28.96 | 3.33 |
その結果CVはやはりA社の方が小さいということになりました。
ポートフォリオのリスクを求める
次に、この2社の株式を保有していた場合、リスクはどの程度分散されるのかについてみていきたいと思います。
| 景気 | A社 | B社 | ポートフォリオ |
| 好況 | 20% | -2% | 9% |
| 通常 | 10% | 10% | 10% |
| 不況 | -2% | 25% | 12% |
そこで、A社とB社、50%ずつ保有するということにして、好況、通常、不況時のリターンを加重平均で表すと、上図のようになります。
その後はこれまでと同様にポートフォリオの期待リターンを算出し、分散を出していきます。
| 景気 | Pリターン | 確率*リターン | 偏差 | 偏差の二乗 | 確率*偏差の二乗 |
| 好況 | 9.00 | 2.7 | -7.3 | 53.29 | 15.987 |
| 通常 | 10.00 | 5.5 | 5.5 | 30.25 | 16.6375 |
| 不況 | 12.00 | 1.8 | 1.8 | 3.24 | 0.486 |
| 期待リターン | 10.00 | 分散 | 33.1105 | ||
最後に冪乗の数値を正の平方根に戻すと
標準偏差は5.75(5.75×5.75=33.1105)
CVは0.58(5.75÷10.00)になりました。
わずか2銘柄でリスクが急減少
驚くほど、リスクが減ったと思いませんか?
A社とB社を買った場合、そのばらつきは両社の平均値になると思っていた人もいるかと思いますが、そうではありません。銘柄を2つに増やすだけで、圧倒的にばらつきが減ったのです。
これが分散化という発想で、株式投資に欠かせない重要な発想です。
分散化とは、資産の正しい組み合わせでリスク低減すること
ただし、注意点は、分散化は、連動性のない資産同士を組み合わせたときにのみ、得ることができる点です。
A社と同じような動きをするC社の株式を持っても、分散効果は得られないということです。
つまり分散化とは、資産を正しく組み合わせることによってリスクを低減すること、なのです。
そう考えると、資産の正しい組み合わせを意識すれば、個別銘柄を購入してもリスクをマネージできるということになります。
なおシステマティックリスクへの対処ですが、抜本的にはオプションや先物の活用以外では、株式への投資配分を減らすほかありません。あとは株式のベータ値が低いものを組み入れるということになりますが、ベータについては別の機会で説明したいと思います。




